la prima ipotesi del teorema di Rolle è la stessa del teorema di Weierstrass, per cui la funzione ammette un massimo e un minimo assoluto nell'intervallo chiuso e limitato Chiamiamo il punto di massimo e il punto di minimo assoluto. Si possono presentano tre casi: primo caso entrambi i punti e sono interni all'intervallo. Vediamo degli esercizi sul teorema di Rolle. Verifichiamo prima le ipotesi e poi andiamo a determinare il valore c per cui f'(c)=0.🎓Vuoi una lezione tutta p.

Teorema Rolle spiegato così facile

PPT Il Teorema di Rolle PowerPoint Presentation, free download ID4246418

Teorema Di Rolle Spiegazione Ed Esercizi Svolti Otosection

LAS MATES DE SANDRA TEOREMA DE ROLLE

Teorema di Rolle ESERCIZI DI MATEMATICA YouTube

Derivata e Teorema di Rolle Esercizi Svolti Periodic Table, Diagram, Youtube, Periodic Table

Teorema di Rolle Spiegazione ed Esercizi Svolti YouTube
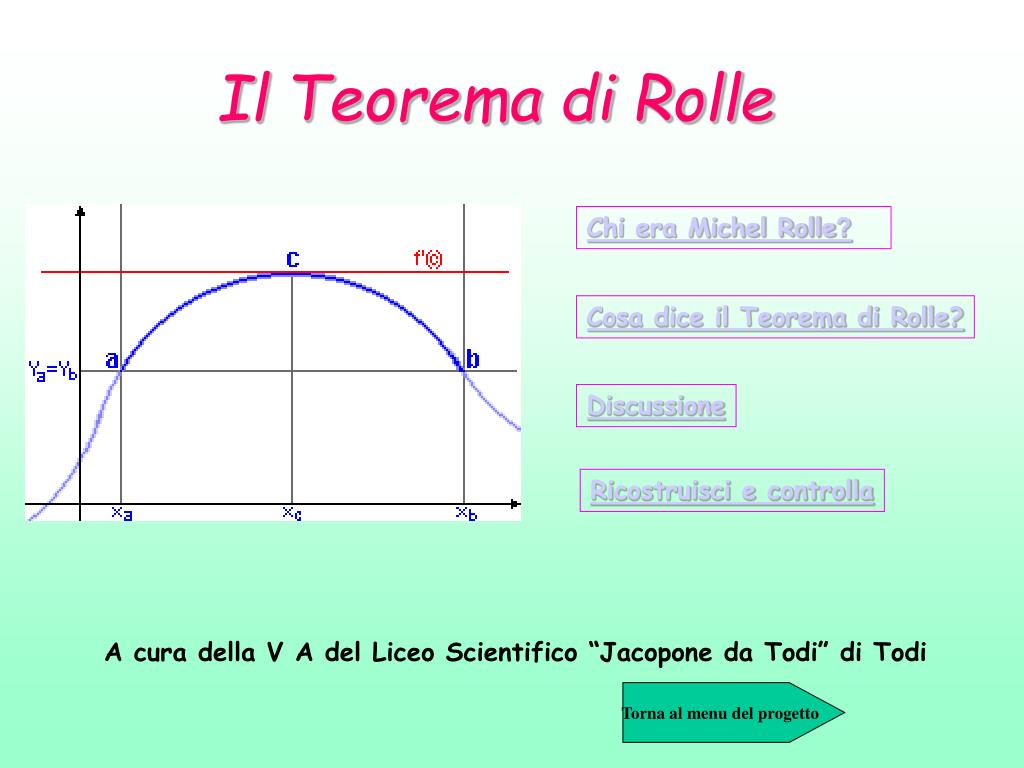
PPT Il Teorema di Rolle PowerPoint Presentation, free download ID4246418

Esercizi sui teoremi di Rolle, Lagrange e Cauchy
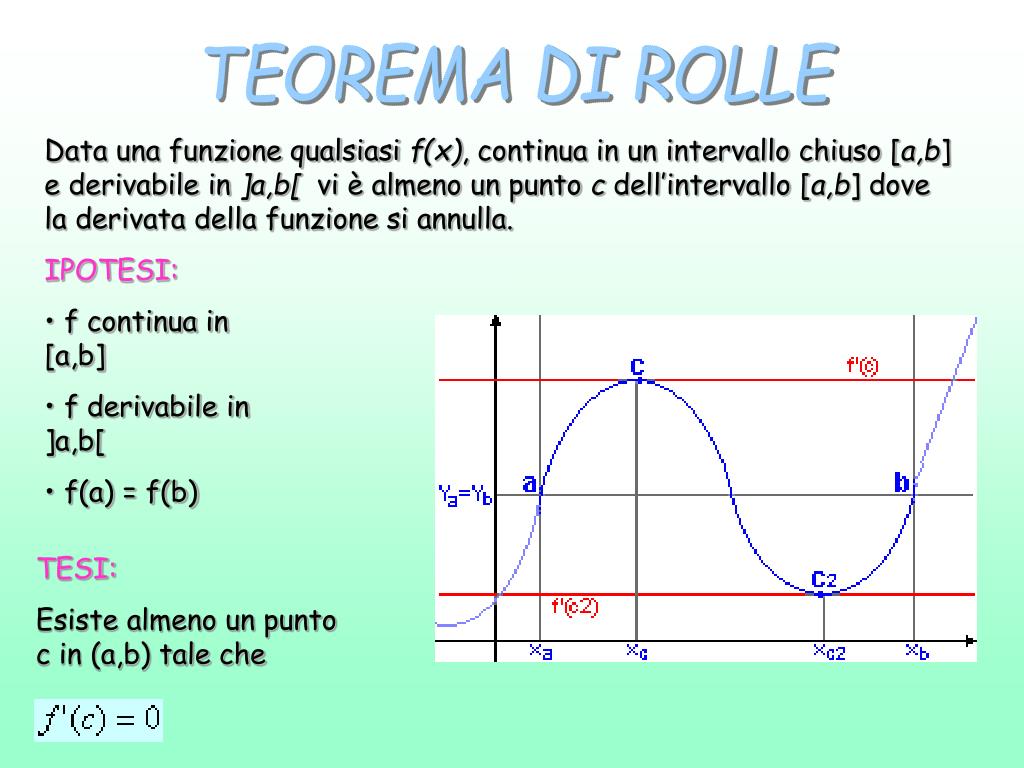
PPT Il Teorema di Rolle PowerPoint Presentation, free download ID4246418

Teorema di Rolle spiegazione ed esercizi tipici YouTube

Il teorema di Rolle. Matematica quarta superiore

PPT Il Teorema di Rolle PowerPoint Presentation, free download ID4246418

O Teorema de Rolle (Parte 1) YouTube

5_esercizio su teorema di Rolle YouTube

TEOREMA DI ROLLE YouTube

Esercizi Teorema Di Rolle Svolti Soluzioni PDF

Teorema di Lagrange e Teorema di Rolle Docsity

PPT Il Teorema di Rolle PowerPoint Presentation, free download ID4246418

SOLUTION Teorema di rolle Studypool
Teorema di Rolle: spiegazione ed esercizi svolti. Il Teorema di Rolle esprime una proprietà fondamentale delle funzioni derivabili. Sia f f una funzione reale di variable reale, definita e continua sull'intervallo chiuso e limitato [a,b] [a,b], derivabile sull'intervallo aperto (a,b) (a,b), e tale per cui f (a) = f (b) f (a) = f (b.. Derivate. Il teorema di Rolle, il teorema di Cauchy ed il teorema di Lagrange sono tre risultati teorici che permettono, partendo da opportune ipotesi ed in riferimento ad un intervallo nel dominio, di ricavare importanti informazioni relative alla funzione. In questa lezione presentiamo i più importanti risultati nell'ambito della derivazione.