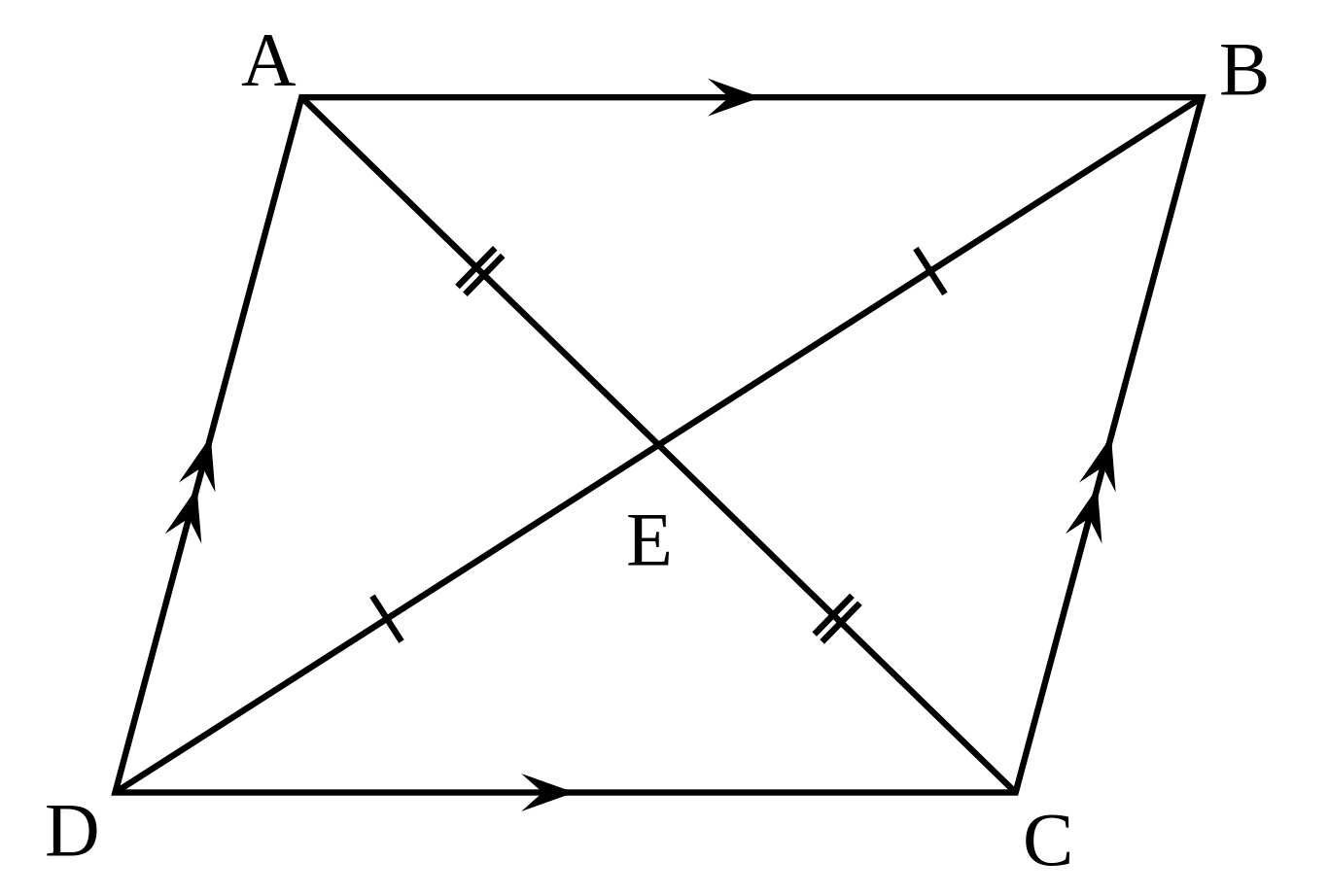
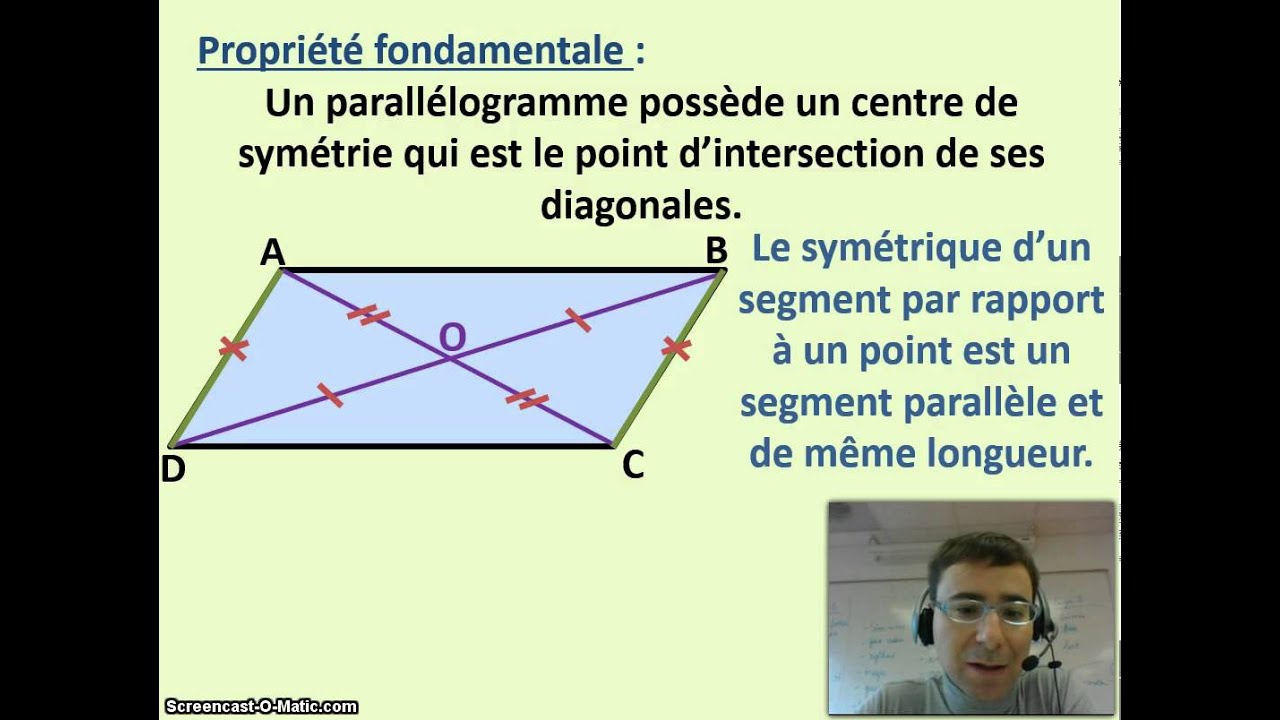
Propriétés du parallélogramme. Voici l'ensemble des propriétés du parallélogramme, puisque. Ses côtés opposés sont de même longueur. Il a ses diagonales qui se coupent en leur milieu. Le point d' intersection des diagonales est centre de symétrie. Ses angles opposés ont même mesure. Ses angles consécutifs sont supplémentaires.. Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux. En général, un parallélogramme ne possède pas d'axe de symétrie. Toutefois sauf s'il est rectangle (comportant des angles droits) ou isocèle (ayant des côtés adjacents isométriques), le parallélogramme comporte deux axes de symétrie.
Définition Parallélogramme

Démontrer qu'un quadrilatère est un parallélogramme YouTube

MNOP est un parallelogramme. M P N = 53° 1. Déterminer, en justifiant, la mesure de l'angle MNO

Comment démontrer que abcd est un parallélogramme avec les vecteurs YouTube

Comment construire un parallélogramme YouTube

Le parallélogramme Cours 1 (FR) AlloSchool
Montrer qu'un quadrilatère est un parallélogramme Parallélogrammes Exercice 5ème
4e Parallélogrammes Cours en vidéos Maths à la maison
Méthode 8 Montrer qu'un quadrilatère est un parallélogramme Mathplace
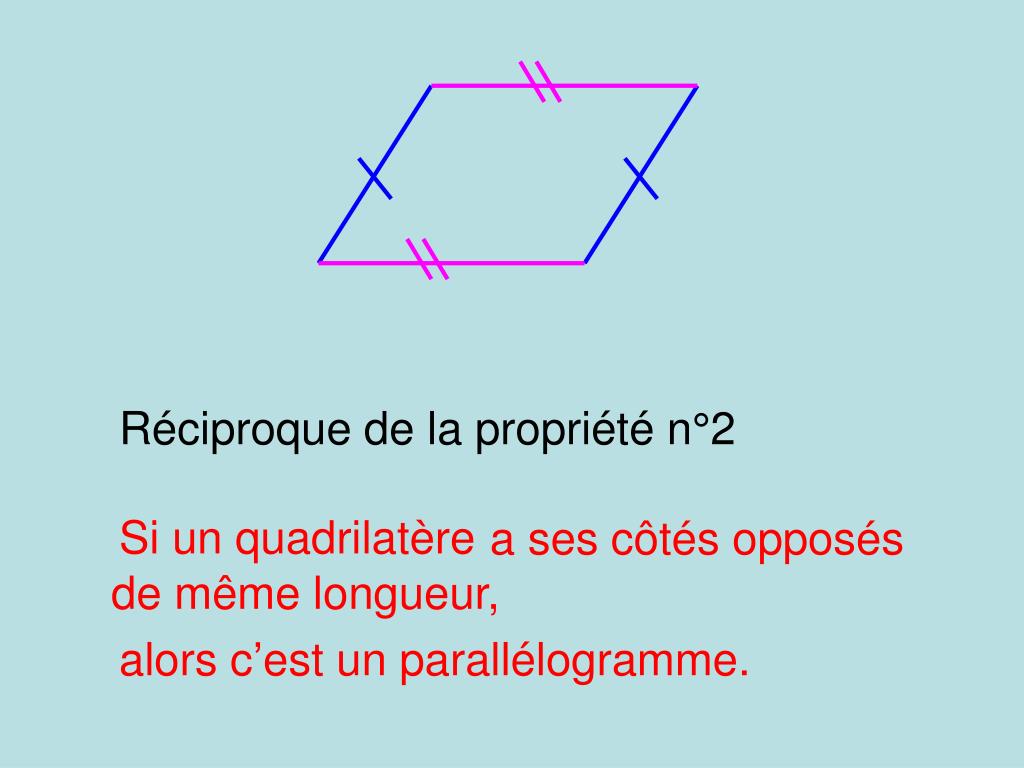
PPT Le parallélogramme PowerPoint Presentation, free download ID4833342

Parallélogramme Vikidia, l’encyclopédie des 813 ans

5G4 2 Montrer qu'un quadrilatère est un parallélogramme YouTube
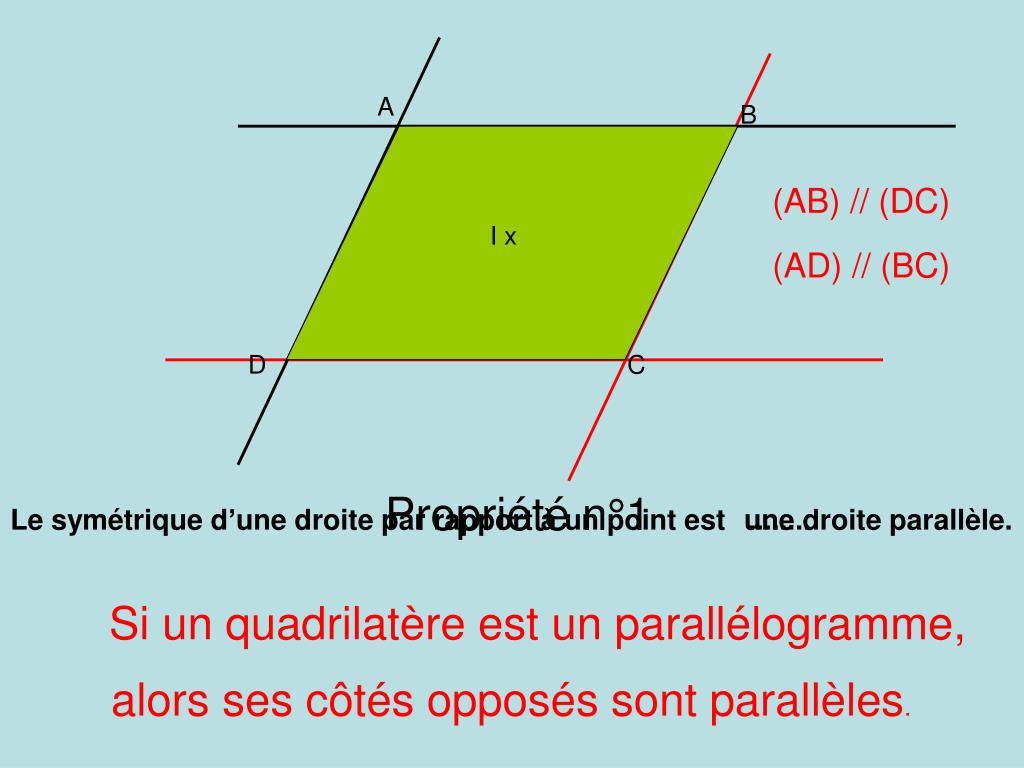
PPT Le parallélogramme PowerPoint Presentation, free download ID4833342

Les parallélogrammes en 5ème Cours, exercices et vidéos maths
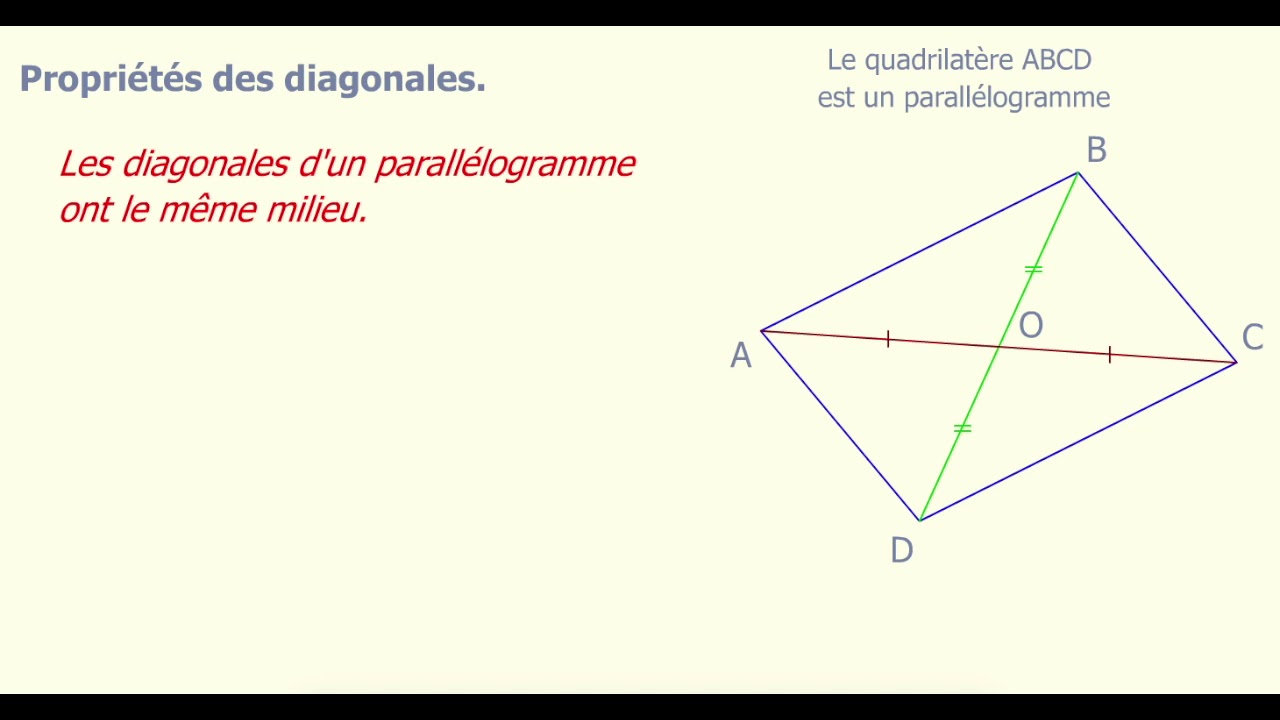
Propriétés des diagonales d'un parallélogramme YouTube

Démontrer un PARALLÉLOGRAMME à partir de propriétés et Chasles Exercice Corrigé Seconde
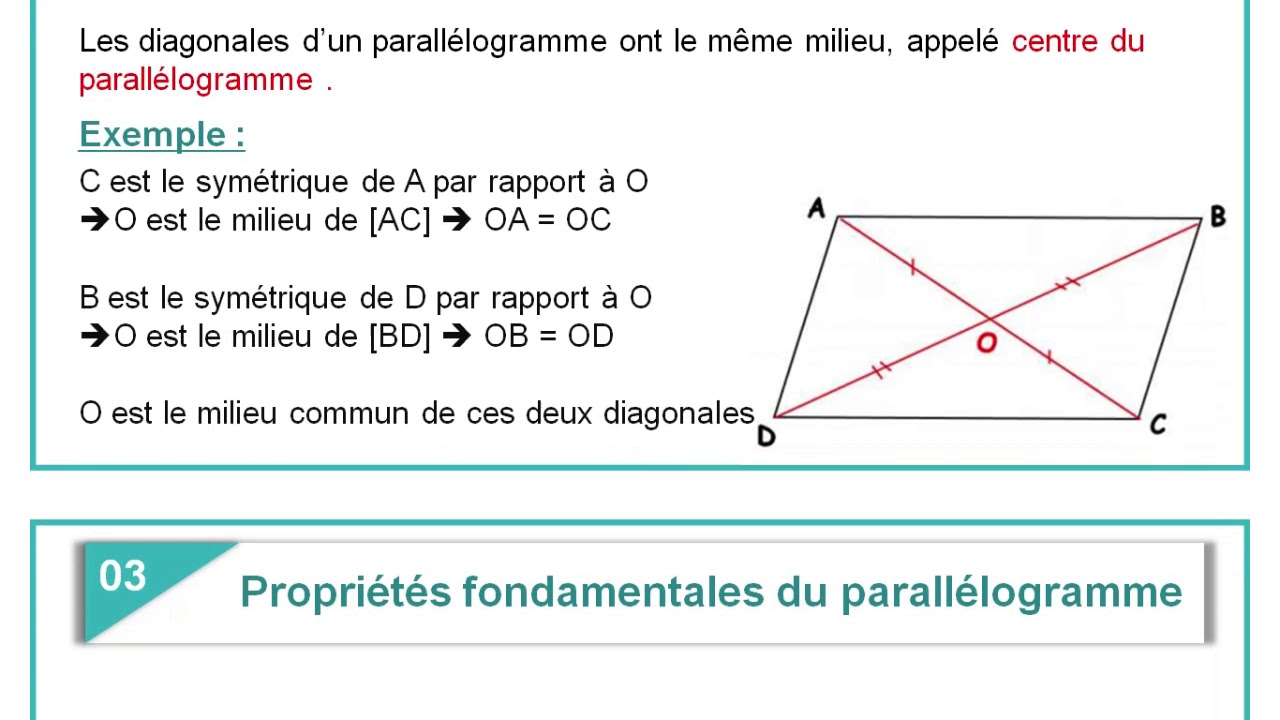
Le parallélogramme (Cours de maths 1AC) YouTube
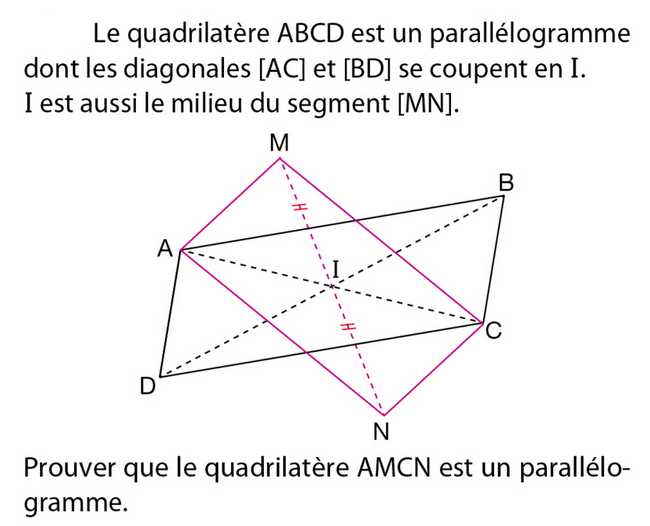
exercice parallélogramme 4ème pdf

Définition du parallélogramme Cours de maths 5ème
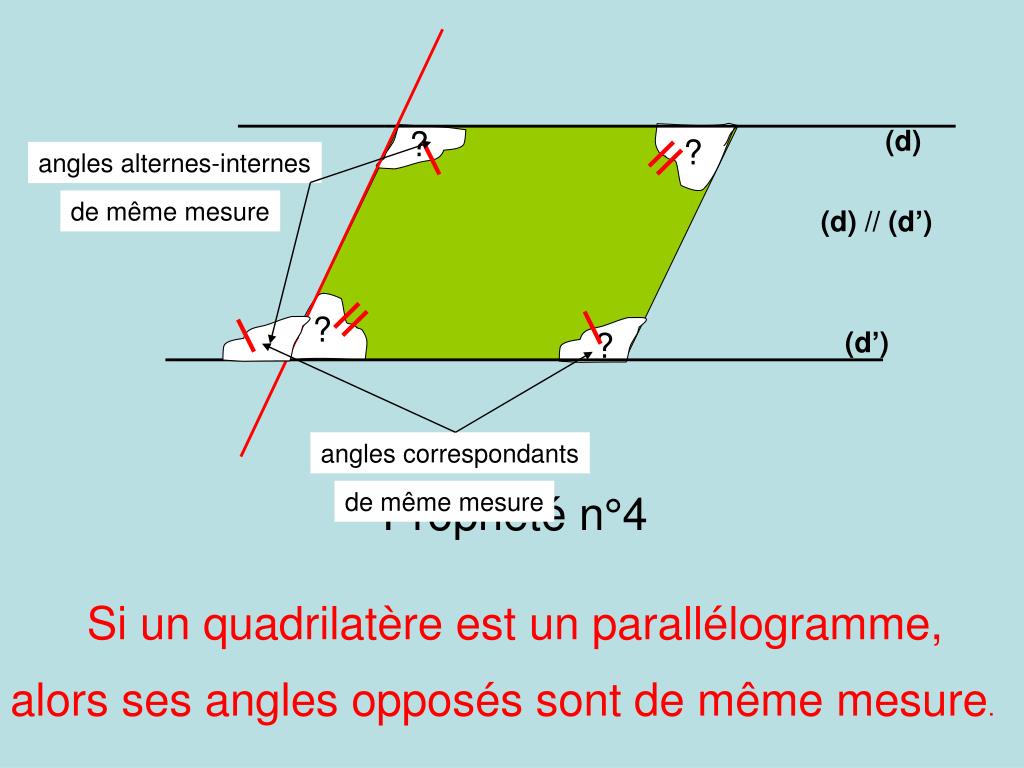
PPT Le parallélogramme PowerPoint Presentation, free download ID4833342
Fiche de cours de maths : Parallélogramme : définition, propriétés, construction. Propriétés: Si un quadrilatère est un parallélogramme, alors : • ses diagonales se coupent en leur milieu • ses côtés opposés sont de même longueur • ses angles opposés sont de même mesure • le point d'intersection de ses diagonales est le centre de symétrie de ce quadrilatère.. L'aire d'un parallélogramme est égale à celle du rectangle de mêmes base et hauteur. Soient la longueur d'un côté du parallélogramme et la longueur de la hauteur associée. L'aire du parallélogramme vaut : L'aire d'un parallélogramme est aussi donnée par un déterminant .