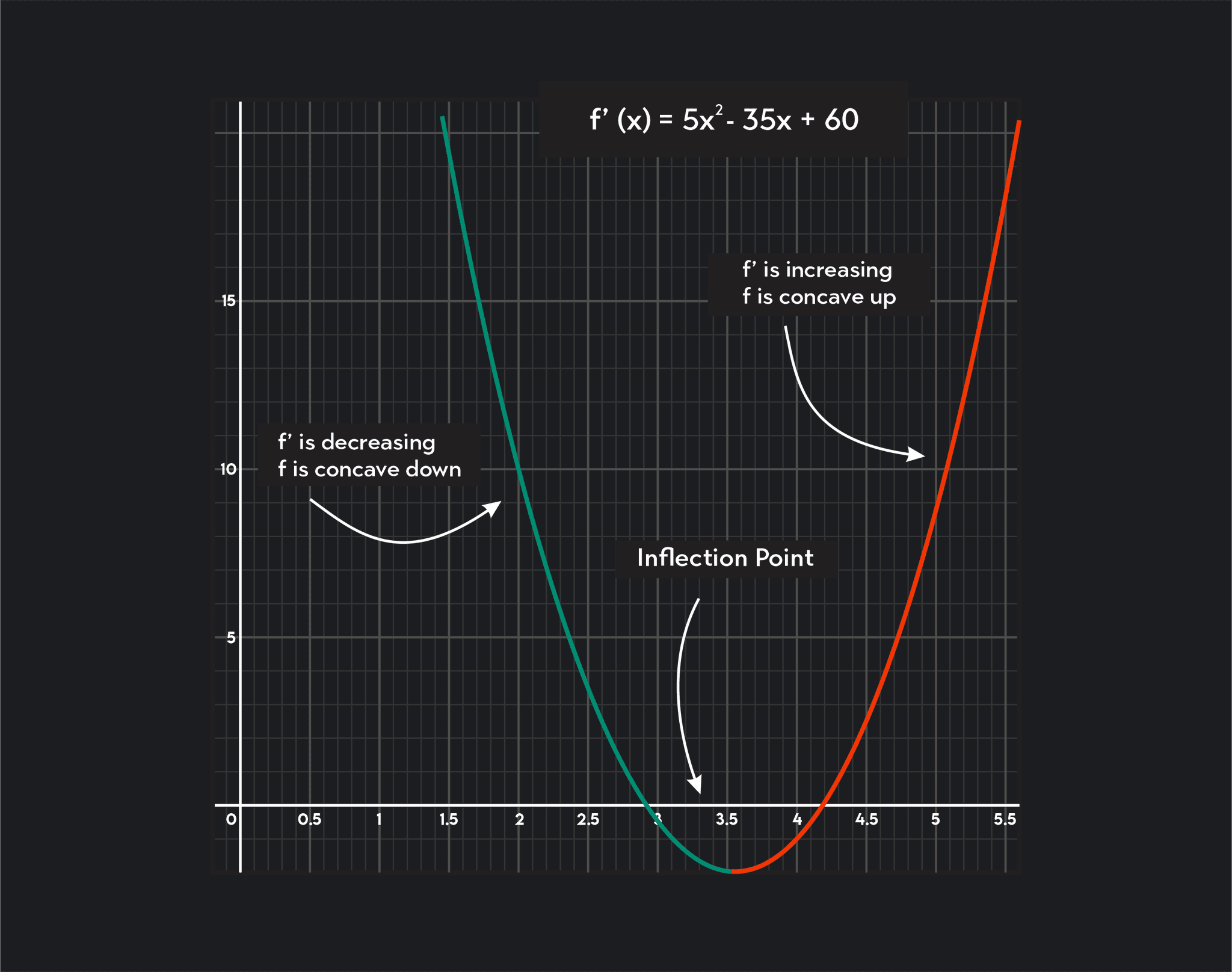
And to find the points of inflection, we set d2y dx2 = 0. ⇒ d2y dx2 = 12x − 10 = 0 ⇒ x = 56. As expected, we have one more stationary point than point of inflection, and this time all our points are real. To determine the order of our stationary points, we calculate the second derivative at x = −13, 2. dy dx = 14 at x = 2 and dy dx.. Summary. A curve's inflection point is the point at which the curve's concavity changes. For a function f (x), f (x), its concavity can be measured by its second order derivative f'' (x). f ′′(x). When f''<0, f ′′ < 0, which means that the function's rate of change is decreasing, the function is concave down.

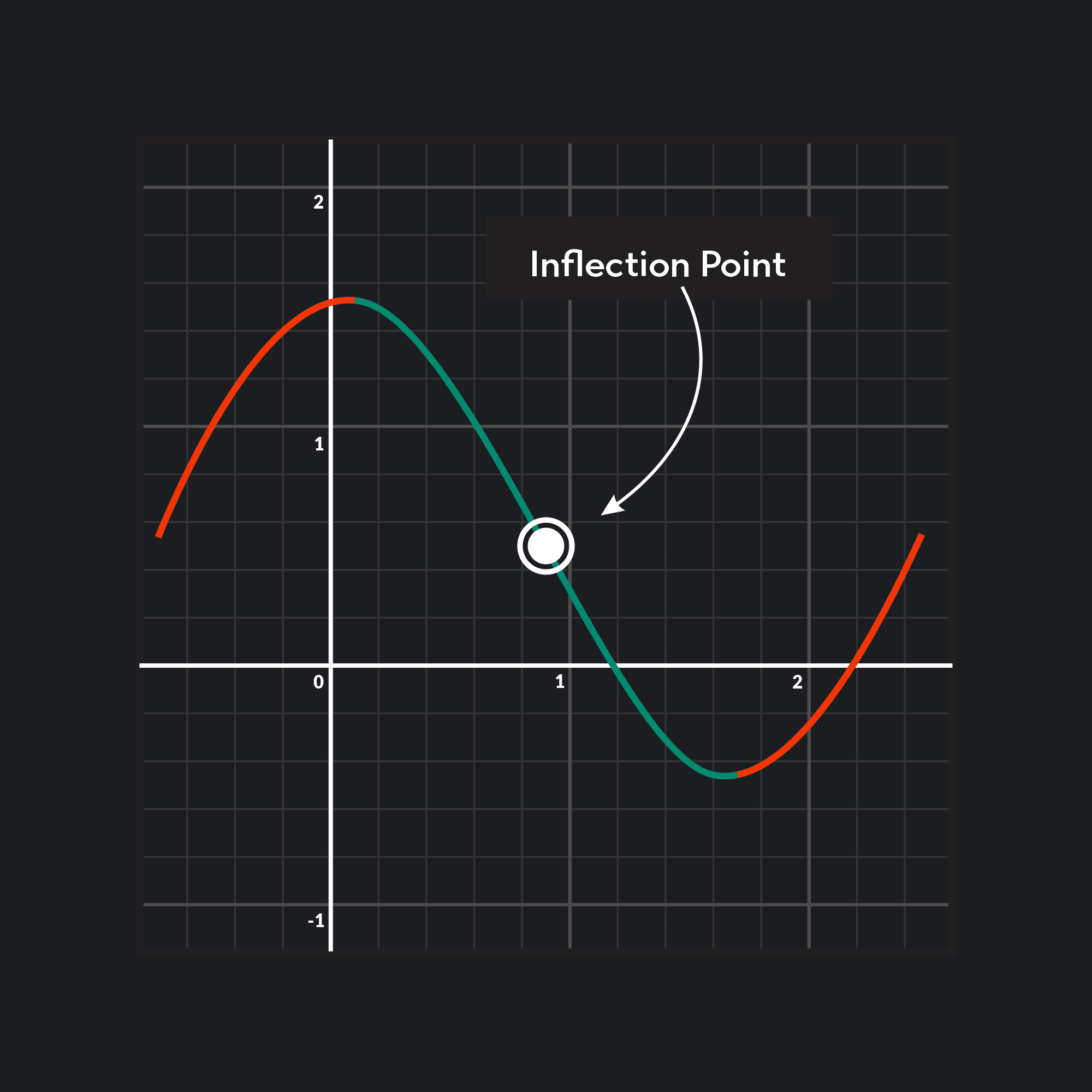
Inflection Point Definition and How to Find It in 5 Steps Outlier

Inflexion Point YouTube

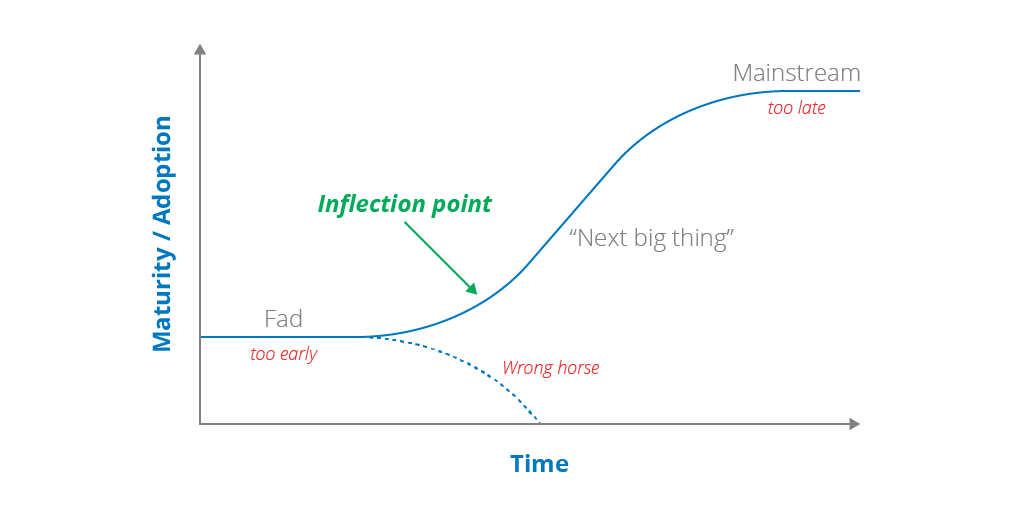
Inflection Points Thoughtworks

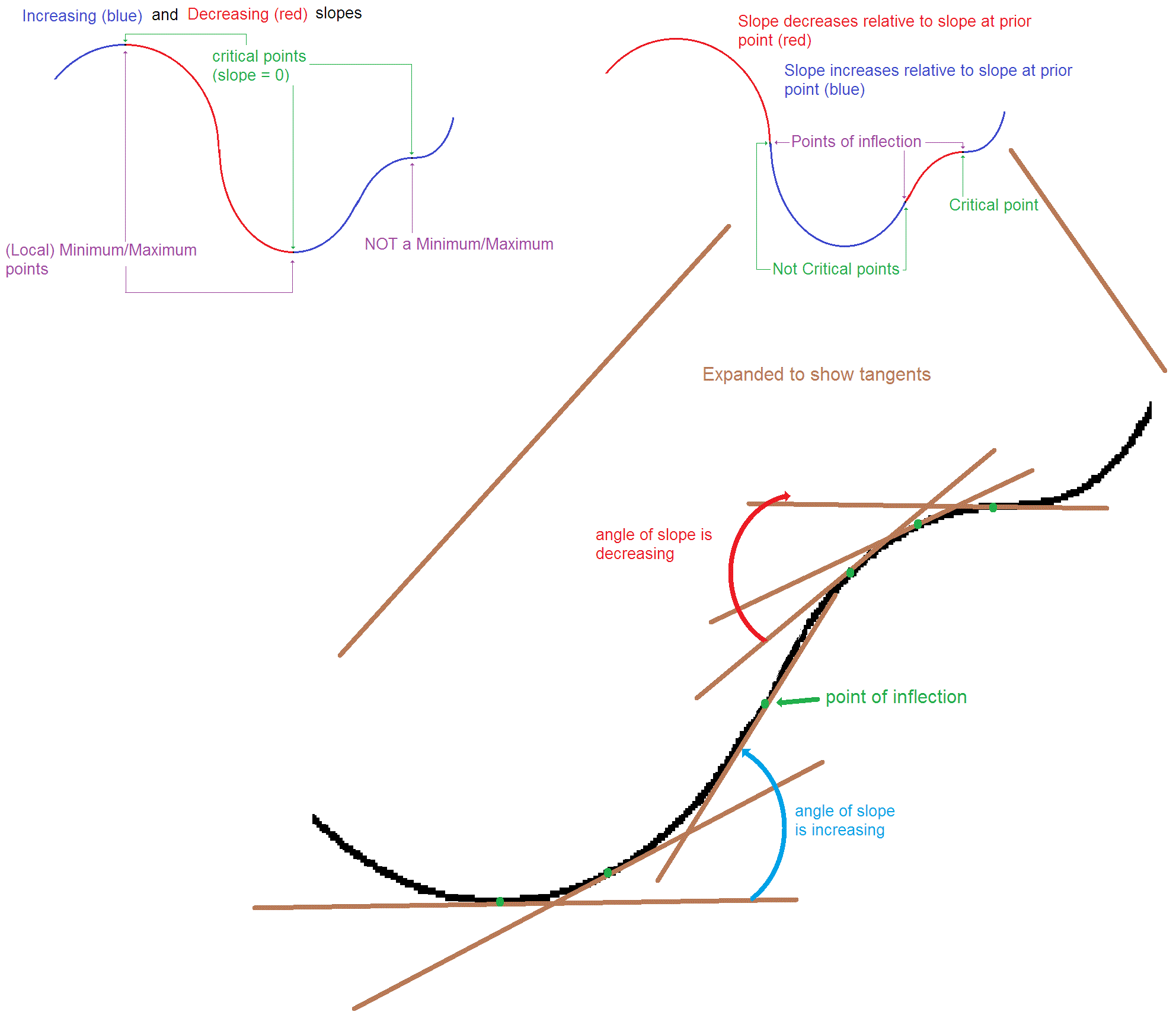
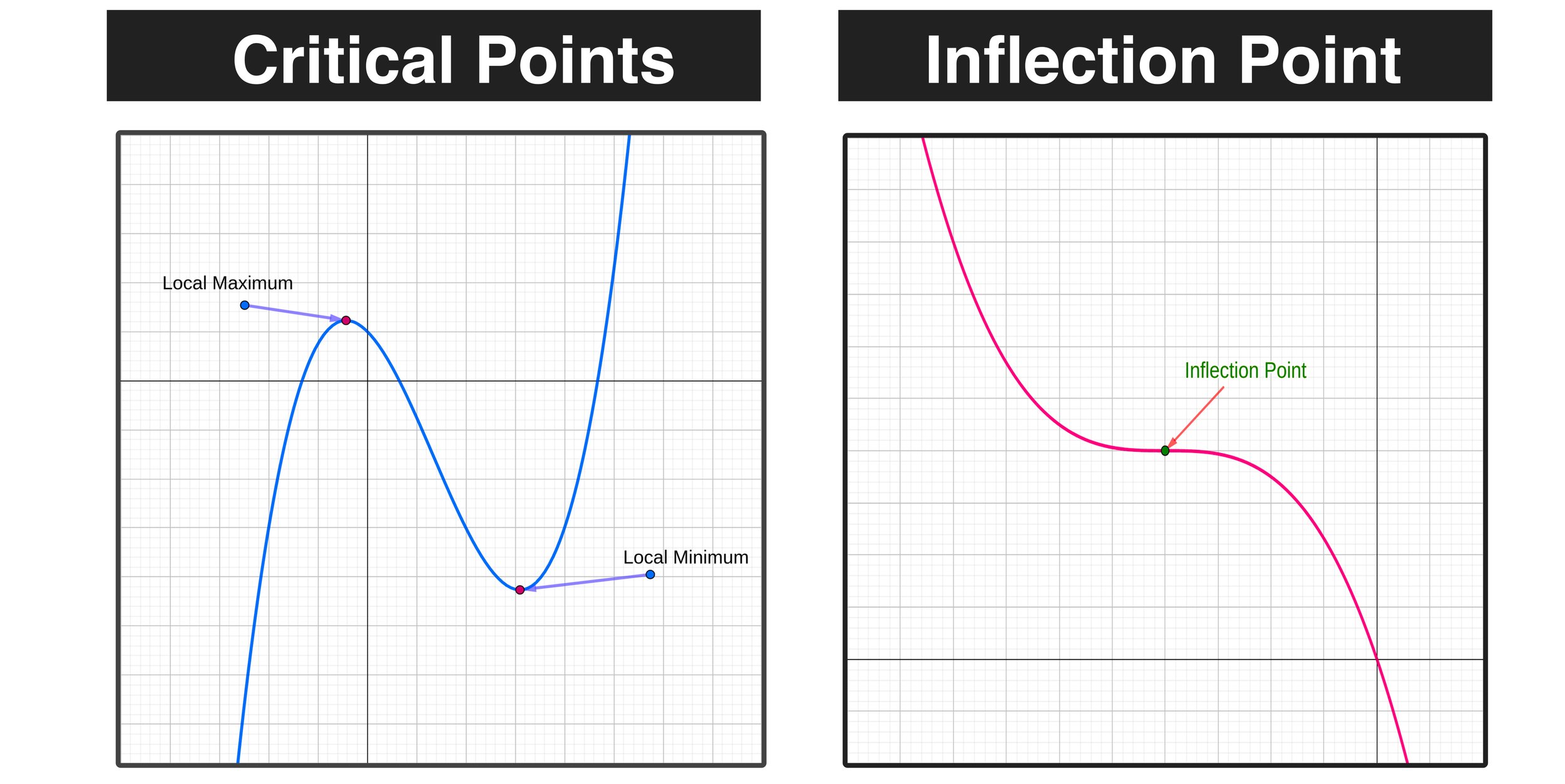
How do inflection points differ from critical points? Socratic

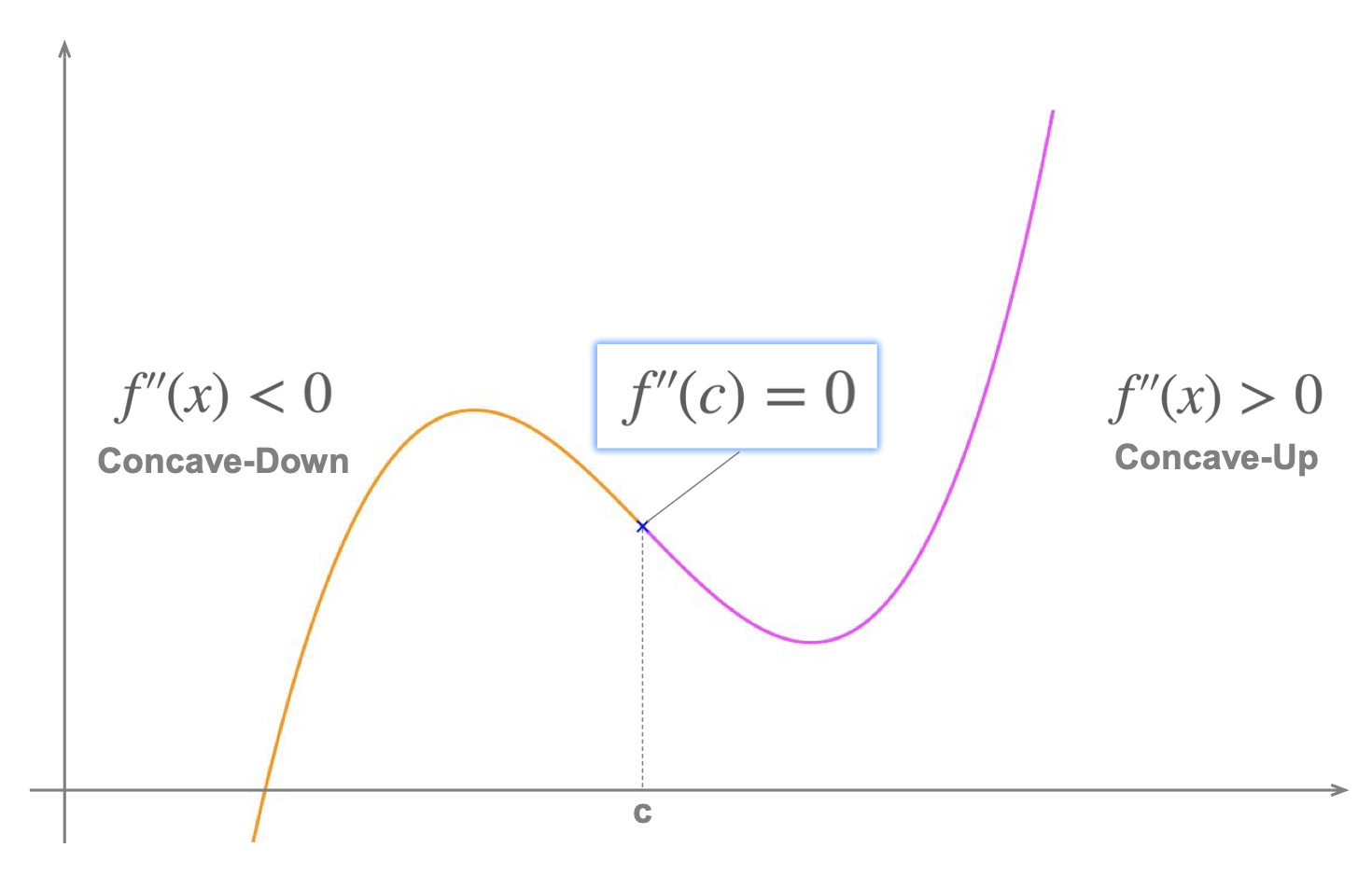
Point of Inflection Calculus

real analysis Reconstructing a function from its critical points and inflection points

Turning Points and Points of Inflection Quadratic, Cubic Graphs Revision for Maths ALevel

How to Find Inflection Points 6 Simple & Easy to Follow Steps

Inflection vs Critical Points YouTube

Inflection Point Definition and How to Find It in 5 Steps Outlier

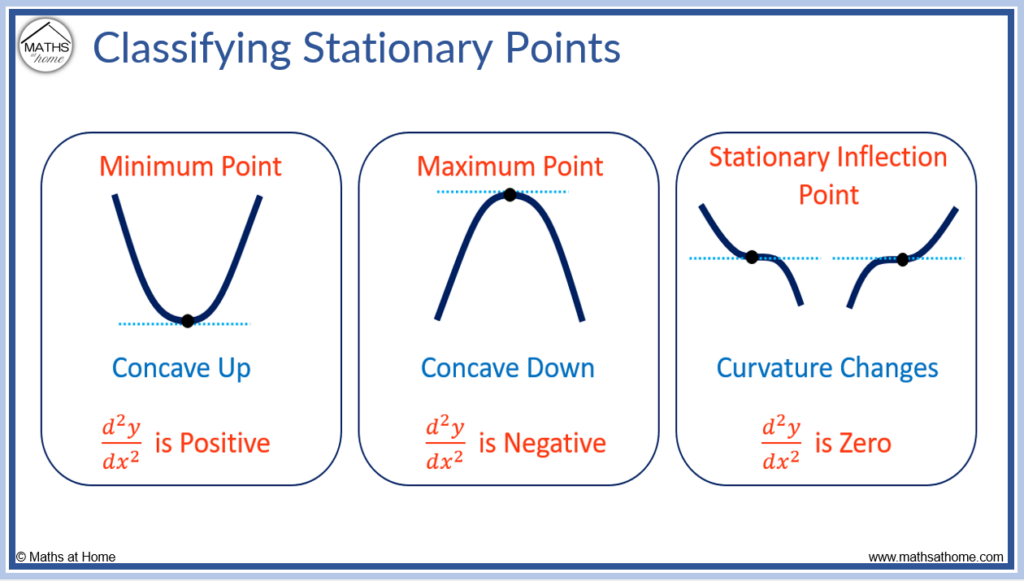
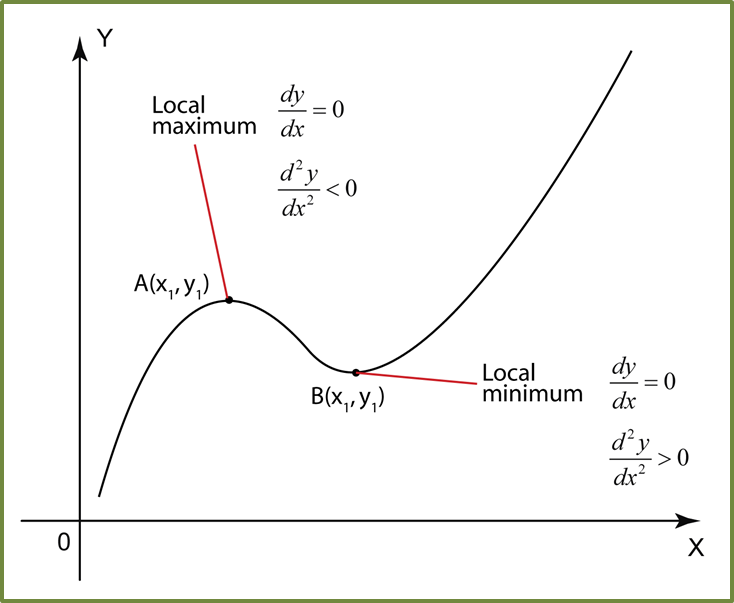
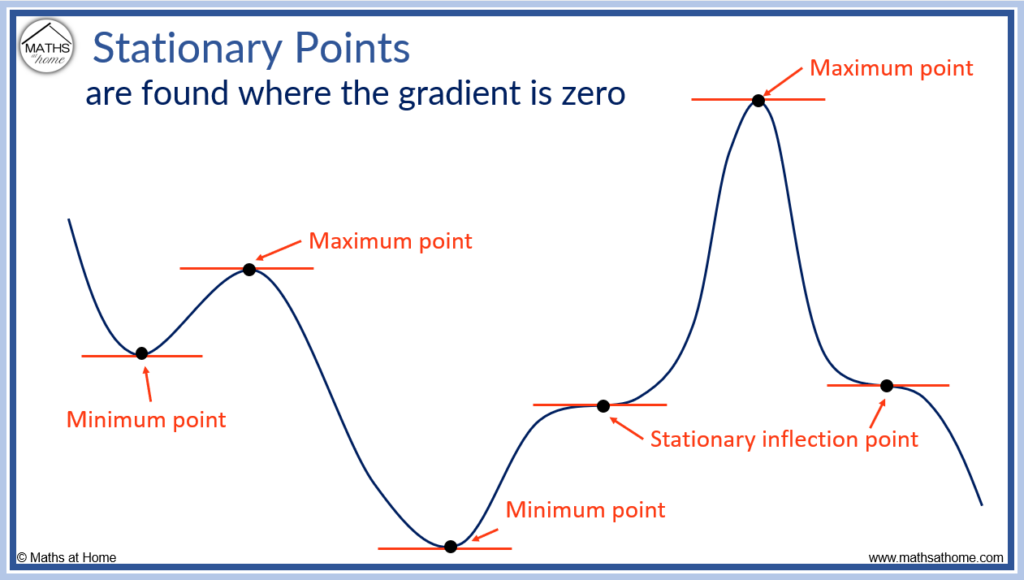
How to Find and Classify Stationary Points

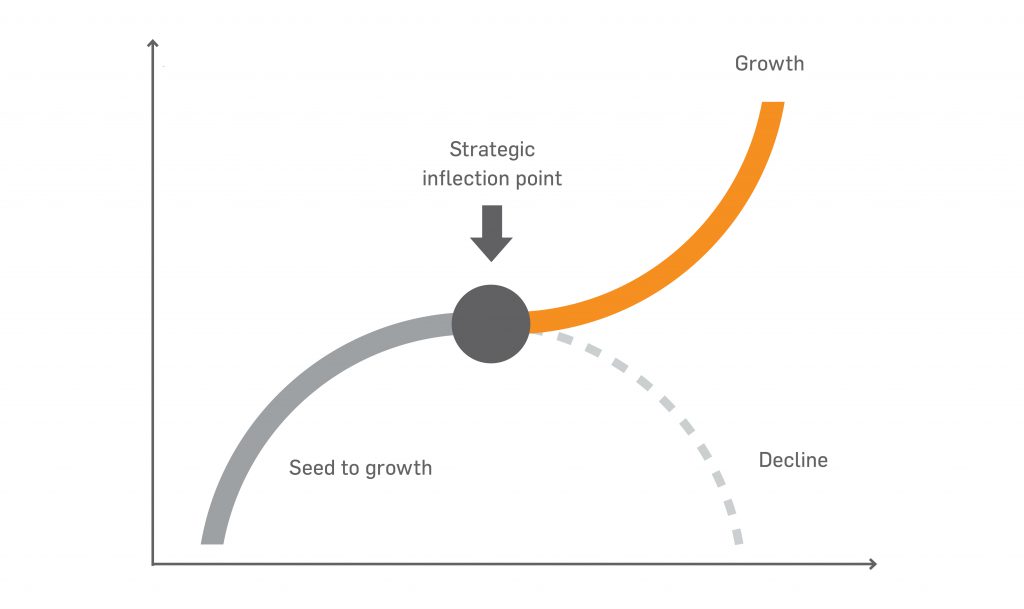
The Hidden Power of Inflection Points Matt Joass

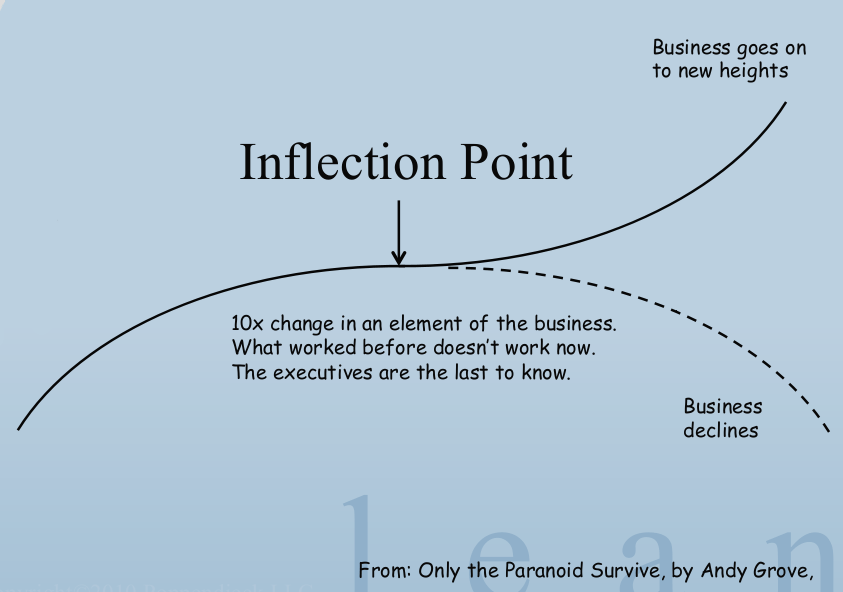
Strategic Inflection Points as defined by Andrew Grove (Intel cofounder) (talk) samim

Stationary points to find local max,min and stationary inflections YouTube

Differential Calculus_Critical Points and Points of Inflection Part I HD 1080p YouTube

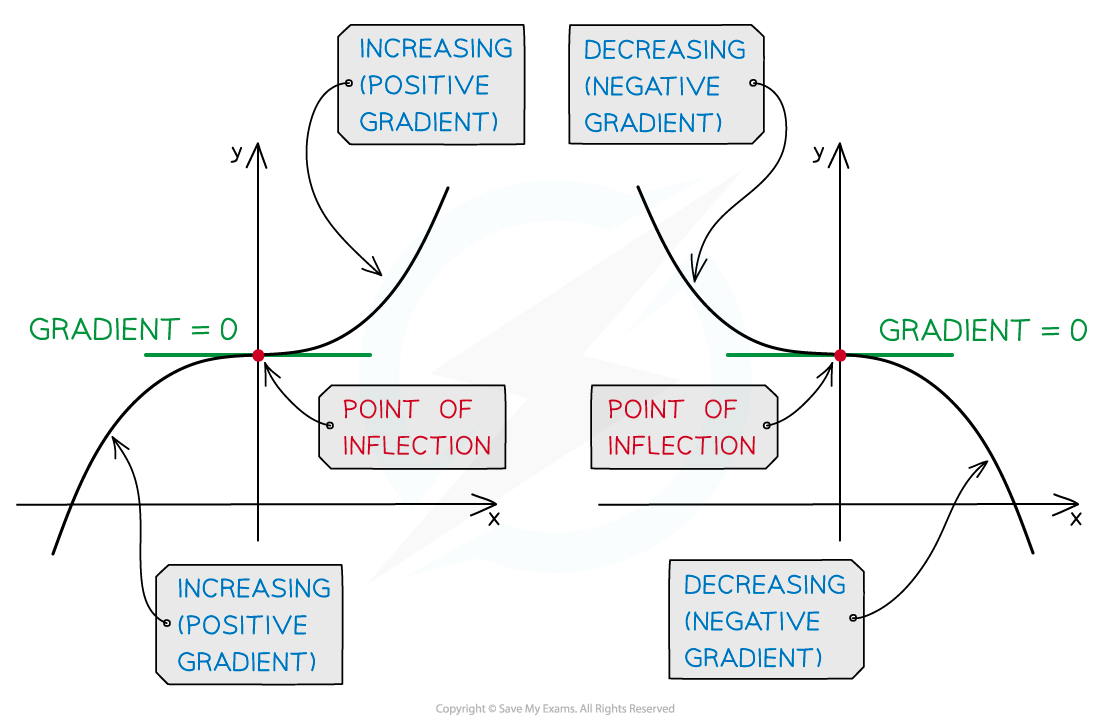
AQA A Level Maths Pure复习笔记7.4.2 Points of Inflection翰林国际教育

9.7 SecondOrder Differentiation, Turning Points, Maximum and Minimum Points user's Blog!

Seven Habits of Highly Inflectious People Interactive

How to Graph a Function in 3 Easy Steps — Mashup Math

نحوه یافتن و طبقه بندی نقاط ثابت

Inflection points are found in a way similar to how we find extremum points. However, instead of looking for points where the derivative changes its sign, we are looking for points where the second derivative changes its sign. Let's find, for example, the inflection points of f ( x) = 1 2 x 4 + x 3 − 6 x 2 . The second derivative of f is f.. Figure 7. Identifying the behavior of the graph at an x-intercept by examining the multiplicity of the zero. The x -intercept \displaystyle x=-3 x = −3 is the solution of equation \displaystyle \left (x+3\right)=0 (x + 3) = 0. The graph passes directly through the x -intercept at \displaystyle x=-3 x = −3. The factor is linear (has a degree.