（小数点以下2位まで） 平方根が自然数の場合、√の中の数字は平方数（自然数の2乗の数字）ということになります。 平方根が整数になる数字. ルート2のルート2乗のルート2乗（2020年横浜市立大学前期理系数学第2問） - 理系のための備忘録. 2021年2月22日 投稿者: pencil. ルート2のルート2乗のルート2乗（2020年横浜市立大学前期理系数学第2問） もうすぐ2次試験ですね! 今回は2020年の横浜市立大から一風変わった証明問題を取り上げます。 以下の問いに答えなさい。 （1） ( 2 2) 2 の値を求めなさい。 （2） 2 が無理数であることを証明しなさい。 （3） x y の値が有理数になる無理数の組 ( x, y) が存在することを証明しなさい。 （2020年横浜市立大学 前期理系第2問） 考え方. 計算自体は容易ですが（3）の考え方が面白い問題です。 普通なら例えば ( 2, log 2.

ルート2をルート2乗してルート2乗する話。あるいは、無理数を使ってx^yを有理数にできるのか？ YouTube

平方根（ルート）の足し算と引き算のやり方と計算問題（中学3年生数学） Irohabook

[B!] かっこのルートを二乗する問題！√を外すだけなので簡単！ 中学や高校の数学の計算問題

【数学】中321 ルートの計算のまとめ 関連する知識の概要ルート 分数

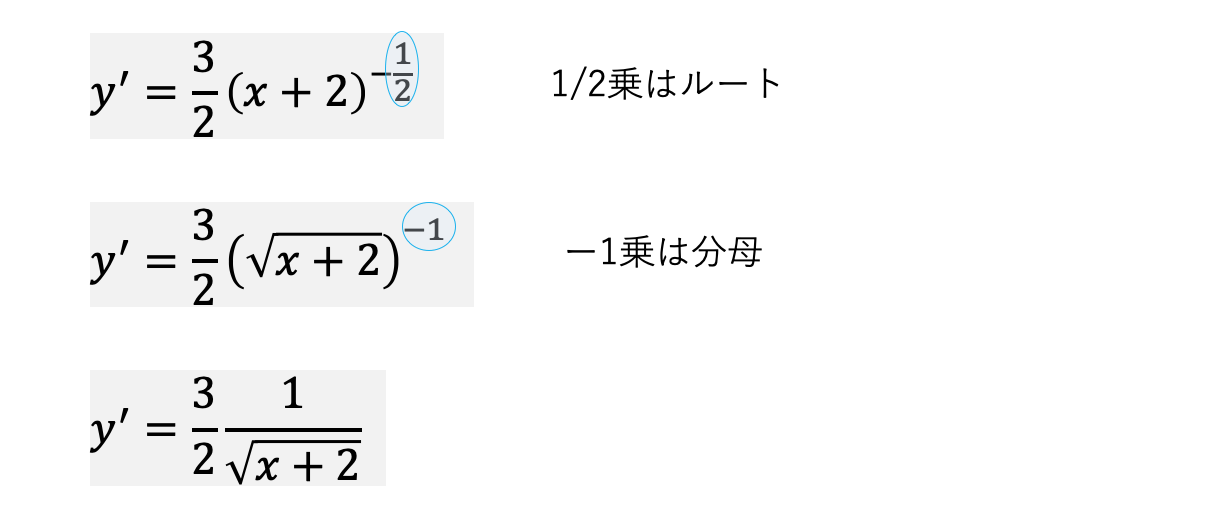
文系の "だいたい" 数学 ルート関数

ルート（根号）の計算方法をマスターしよう！｜スタディクラブ情報局

[最も好ましい] 数学 ルート 問題 321154数学 ルート 問題 Josspixtrmw

数学のルートの分数の二乗 この式の計算方法を教えてください。 OKWAVE

ルートの中身を小さくする問題 あんず学習塾のメモ・図表置き場

2のルート2乗を卓上電卓で求める 怜悧玲瓏 ～高校数学を天空から俯瞰する～

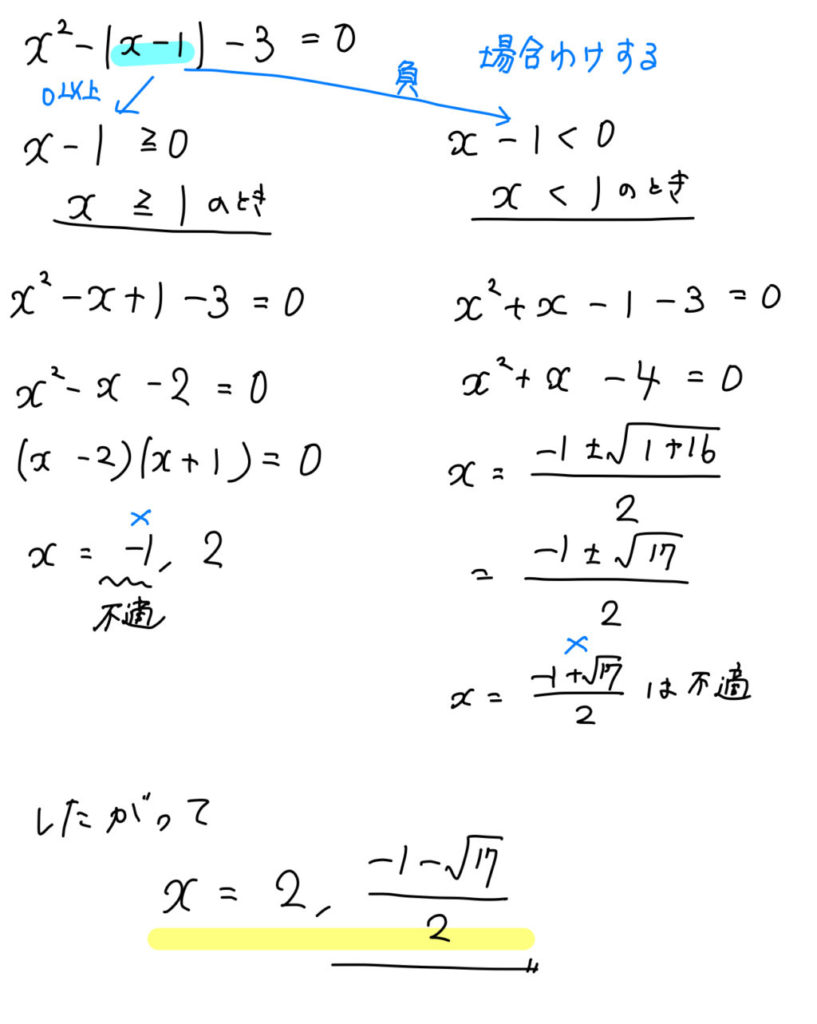
分数、小数、ルートを含む二次方程式の解き方まとめ！ 数スタ

1/2乗って何？ どうしてそれがルート（平方根）になるのか 数学の面白いこと・役に立つことをまとめたサイト

[B!] 計算を簡単にする方法！二乗の展開公式を使うと掛け算が楽！ 中学や高校の数学の計算問題

2のルート2乗を卓上電卓で求める 怜悧玲瓏 ～高校数学を天空から俯瞰する～

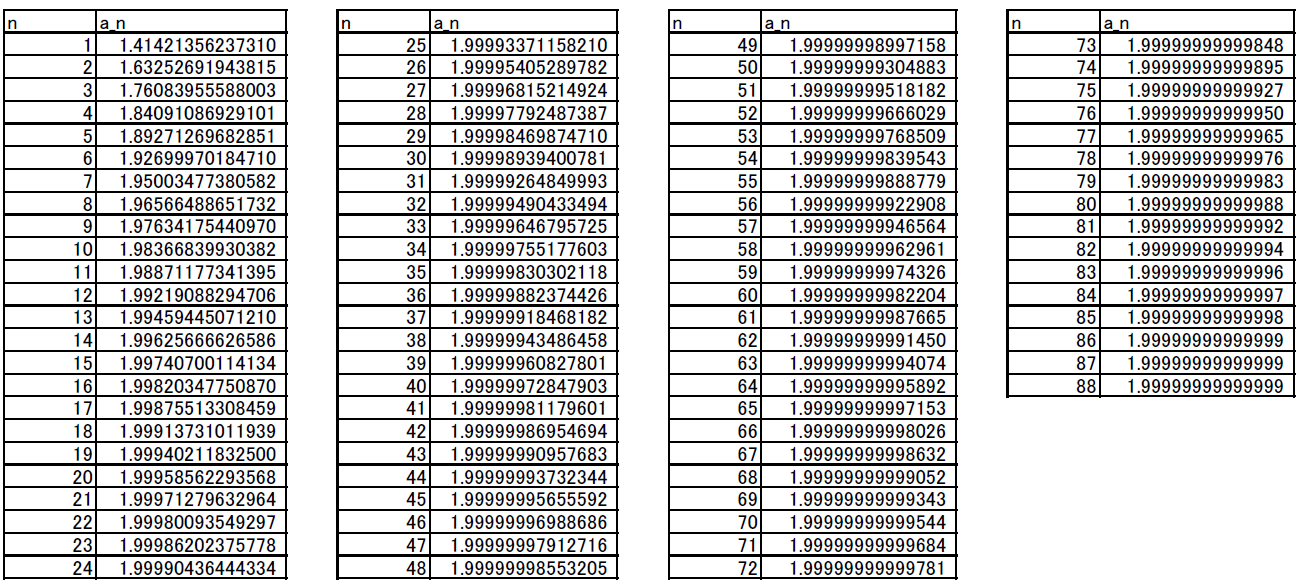
高校数学の発展 ルート2のルート2乗のルート2乗のルート2乗の・・・

2のルート2乗を卓上電卓で求める 怜悧玲瓏 ～高校数学を天空から俯瞰する～

2乗を使って考える！ルートを含む不等式の証明をイチから解説！ 数スタ

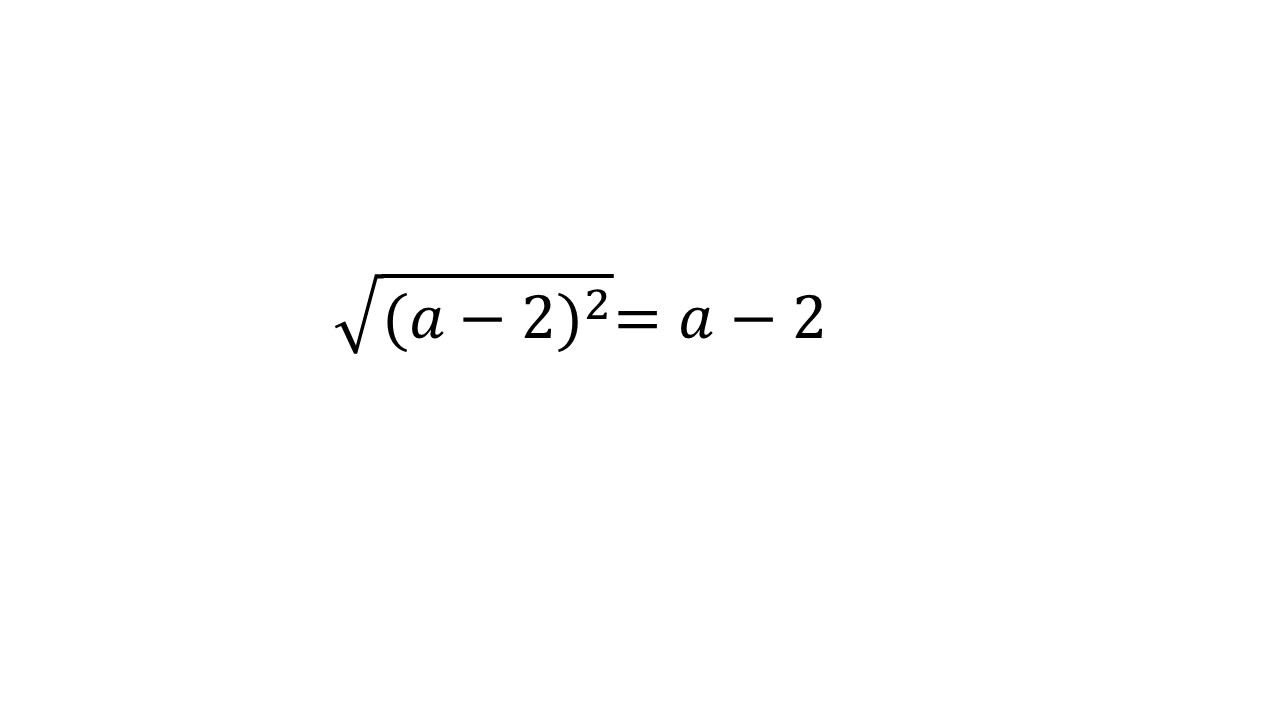
根号（ルート）の中に2乗があるときの対処法（根号（ルート）は「正の平方根」という意味です） 大学受験の王道

ルートの式の値の求め方をイチから！x2乗＋y2乗の値はどうする！？ YouTube

ルートの中に2乗があるとき 大学受験の王道

解答・解説. (1) ( 2-√ 2√) 2√ の値. ( 2-√ 2√) 2√ = ( 2-√) 2√ × 2√ = ( 2-√)2 = 2. (2) 2-√ が無理数であることを証明. 2-√ が有理数であると仮定する. 互いに素な自然数 a, b を用いて. 2-√ = a b とおける．. よって a = 2-√ b. 両辺を2乗して、 a2 = 2b2 ・・・ ①. よって、 a2 は2の倍数であるから、 a も2の倍数 ・・・ ② である．. 自然数 k 用いて、 a = 2k とおける．. a = 2k を①に代入して、 4k2 = 2b2. つまり b2 = 2k2. よって、 b2 は2の倍数であるから、 b も2の倍数 ・・・ ③ である.. ルート2のルート2乗について $\sqrt{2}^{\sqrt{2} }$ は、もはやどんな数なのか、手で計算して具体的に求めるのは難しいです。 また、 $\sqrt{2}$ が無理数であることの証明で使ったように、「有理数だと仮定すると、どこかで矛盾が生じる」というのも.